No hemos encontrado resultados relativos a la búsqueda realizada.
Puedes volver a intentarlo de nuevo realizando una nueva búsqueda.
No hemos encontrado resultados relativos a la búsqueda realizada.
Puedes volver a intentarlo de nuevo realizado una nueva búsqueda.
Aplicación de Voronoi en algoritmos no supervisados de Machine Learning con análisis geoespacial
Por Diego Alessandro Fonseca Zalazar

03 de Ago de 2023 · Informática y TICS
El presente proyecto de investigación pretende abordar la temática del análisis geoespacial y la aplicación de algoritmos no supervisados de Machine Learning. El objetivo principal es estudiar la delimitación y agrupación de datos en un contexto geográfico utilizando el algoritmo de Voronoi en conjunto con algoritmos no supervisados como K-Means y DBSCAN. Para ello, se utilizan librerías de Python como geopandas, scikit-learn, scipy y matplotlib para el procesamiento y visualización de datos. El problema que se pretende resolver con este trabajo es identificar patrones espaciales y segmentar datos geográficos relevantes en diferentes grupos (clústers) que pueden ser estudiados individual o conjuntamente, para obtener información implícita, es decir, la información realmente contenida en el grupo de datos. Esto permite que los datos se estudien en base a la información relacionada a los datos y no dependa de la división territorial per se, aislando el ruido de estos al ser estudiados en base a limitaciones históricas y/o políticas. Así, la información implicita en los distintos grupos de datos puede ser un complemento analítico de estrategia empresarial.
Es por ello que, este proyecto de investigación usa el ejemplo de establecer una nueva empresa dentro de un territorio (Chamberí), usando los datos para construir clústers y establecer relaciones espaciales que puedan ayudar a la toma de decisiones en ámbitos como el urbanismo, el marketing y la planificación territorial, siendo estos potenciales objetivos parte relevante del análisis estratégico empresarial.
¿Te resulta interesante?
¡Guarda este contenido completo en PDF!
Descarga gratis este contenido y consúltalo cuando lo necesites
1. Introducción
Si bien los algoritmos de geometría computacional son conocidos en las distintas carreras relacionadas a la informática, la información referente a su integración con técnicas de Machine Learning es más bien escasa, o levemente referenciada, más no explorada en profundidad.
El algoritmo más útil para aplicarlo en Machine Learning no supervisado es el algoritmo de Voronoi, por ello, esta investigación pretende profundizar en su utilidad como herramienta complementaria a los algoritmos no supervisados, enfocando dicha aplicación sobre diferentes tipos de datos dentro de un diagrama geoespacial.
2. Fundamentación Teórica
2.1. Algoritmos
Aunque a menudo se hace uso de KMeans y KNN justificadamente, al ser los algoritmos de Machine Learning no supervisados más habituales, no se debe ignorar que otros tipos de algoritmos pueden tener ventajas computacionales o analíticas frente a los algoritmos anteriormente mencionados.
Por ejemplo, si se tiene un proyecto en el que se busca identificar el ruido dentro del conjunto de datos que están entre o alrededor de los clústers la elección de KMeans y KNN sería errónea ya que estos no son algoritmos para identificar el ruido como si lo puede hacer DBSCAN y OPTICS siendo estos similares entre sí, pero cuya diferencia principal radica en que DBSCAN usa un algoritmo de densidad mientras que OPTICS usa uno de proximidad, además DBSCAN es computacionalmente más rápido que OPTICS, por lo que, puede funcionar mejor para proyectos con un gran volumen de datos.
Por este motivo, la clasificación de los algoritmos es importante, ya que la eficiencia del modelo de datos que tengamos en mano a estudiar será más o menos eficiente según el tipo de algoritmo que escojamos y de cómo optimizamos sus parámetros en caso de que estos sean paramétricos, esto debido a que si dichos parámetros no se adecuan al conjunto de datos nuestro modelo presentará problemas como los que se mencionaron anteriormente para el caso de KMeans siendo los más habituales la asignación de peso distinto entre los datos, la mala selección de cantidad de clusters y la distribución anisotrópica de los datos.
2.2. Voronoi
Los diagramas de Voronoi forman parte de los algoritmos fundamentales en el campo de la geometría computacional, en este caso más específicamente es un algoritmo de interpolación que resulta en un diagrama en base a una nube de puntos, y con ella, se estudia la proximidad de dichos puntos.
A partir de la distancia entre un par de puntos p y q se obtiene la media de la distancia || p - q || y con ello es posible trazar una recta en el diagrama que divida ambos puntos, este cálculo de medias repetido recursivamente en cada uno de los puntos comparándolos entre sí da como resultado la generación del diagrama de Voronoi formado por los vértices como intersección entre dichas líneas formadas a partir de || p - q || y la región de Voronoi como resultado de la unión de dichos vértices. Esta región es la que posteriormente se usará como una visualización de la división geométrica de un clúster.
Figura 1. Voronoi diagram in a plane
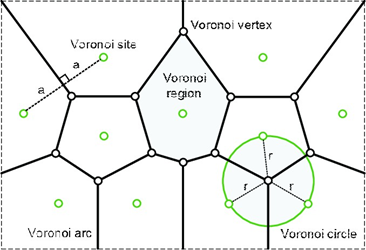
Fuente: Galishnikova, V. & Jan Pahl, P. (2018)
Con este tipo de diagrama se puede estudiar la proximidad entre un punto y los puntos de Voronoi, los cuales a partir de estos se obtiene todo el diagrama. Esto mismo podemos aplicarlo en los algoritmos de aprendizaje no supervisado de Machine Learning, convirtiendo los centroides como los puntos de Voronoi que se necesitan para poder hacer el diagrama entero sobre la visualización obtenida por un algoritmo no supervisado.
Esto es aplicable porque sigue una lógica clara: si se obtiene una nube de puntos con la cual formar un clúster en Machine Learning, de estos puntos se puede obtener su centroide y con ello aplicar esta técnica de geometría computacional.
2.3. Normas generales
Teniendo en cuenta un conjunto de datos P, cuyos datos forman parte del conjunto a modo de P1, P2, P3...Px, entonces:
- Los puntos del conjunto P representan datos discretos.
- Los datos de P pueden usarse en un algoritmo no supervisado de Machine Learning.
- La representación gráfica de este conjunto aplicado a un algoritmo sirve como base para el modelado de un diagrama de Voronoi, esto con el fin de obtener una serie de clústers que definan dicho modelo.
- A partir de las regiones de Voronoi formadas por los clústers, se puede profundizar en la información contenida en dicho clúster como una forma de separar el espacio geográfico.
- Con la información que se pueda extraer de las regiones de Voronoi y clústers, se pueden realizar cálculos con los cuales mejorar el entendimiento de los datos y su contexto, con el fin de realizar conclusiones sobre dichos datos.
2.4. Explicación y funcionamiento
El diagrama de Voronoi tiene múltiples aportes a los algoritmos de aprendizaje no supervisado en Machine Learning, siendo estos aportes principalmente:
- Trazar y comparar regiones de Voronoi con lo cual hacer seguimiento del comportamiento de los grupos y su pertenencia comparativa con los clúster más cercanos.
- Permite al analista de datos tener en mente una clara posibilidad de pertenencia de un punto a un determinado clúster u otro, a pesar de que esta información aún no esté dada.
- Estudiar la proximidad y los límites entre los diferentes centroides que conforman un clúster.
- Uso de los vértices como elemento geométrico para visualizar la zona común que existe entre un grupo de clústers próximos entre sí y separados cada uno por una región de Voronoi.
- A partir de los espacios vacíos generados en un diagrama de Voronoi, verificar si se cumple el tercer teorema, y estudiar la posible existencia de potenciales nuevos grupos por segmentar en la visualización de la clusterización.
3. Ejemplificación
Con el fin de aplicar esta serie de "reglas" a un caso práctico para hacer más ilustrativa la explicación, se usarán datos reales sobre bares en el municipio de Chamberí, y a partir de dicha información se usarán los algoritmos para profundizar más en dicha información se buscará llegar a una conclusión: Teniendo en cuenta los datos ¿En que zona de Chamberí sería mejor establecer un nuevo bar?
Código:
#DATOS Y ALGORITMOS
#Importación de librerias import matplotlib.pyplot as plt import osmnx as ox
from scipy.spatial import Voronoi, voronoi_plot_2d from sklearn.cluster import KMeans
import pandas as pd
#Mapa del distrito de Chamberí
distrito = ox.graph_from_place('Chamberí, Madrid, Spain', network_type='drive') streets_graph = ox.projection.project_graph(distrito)
streets = ox.graph_to_gdfs(ox.get_undirected(streets_graph), nodes=False, edges=True, fill_edge_geometry=True)
puntos = pd.read_csv('/home/usuario/documentos/mapeado.csv', header=None) #Datos
km = KMeans(n_clusters= 4, random_state=0).fit(puntos) #Modelo KMeans
#VISUALIZACIÓN DE MAPA Y ALGORITMOS
#crear el gráfico
f, ax = plt.subplots(figsize=(9, 9))
xmin, xmax = streets.total_bounds[0], streets.total_bounds[2] ymin, ymax = streets.total_bounds[1], streets.total_bounds[3] ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
streets.plot(ax=ax, color='blue', alpha=0.5, zorder=1) # agregar el mapa de calles al gráfico #Visualización de puntos y centroides
centers = km.cluster_centers_
plt.scatter(puntos[0], puntos[1], c=km.labels_, s=100) plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, marker='*') plt.scatter(puntos[0], puntos[1], c=km.labels_, s=10, cmap='viridis')
#Voronoi
vor = Voronoi(centers)
voronoi_plot_2d(vor, ax=ax, show_vertices=True)
#Etiqueta y visualización final plt.xlabel('Longitud') plt.ylabel('Latitud')
plt.show()
# mostrar el gráfico
plt.show()
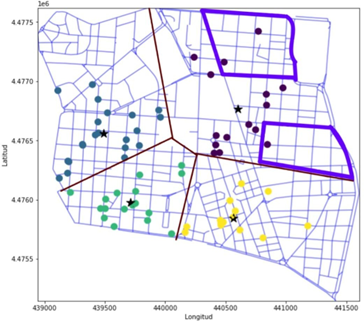
Figura 2. Mapa de bares en Chamberí usando OSMNX y KMeans optimizado a cuatro clústers
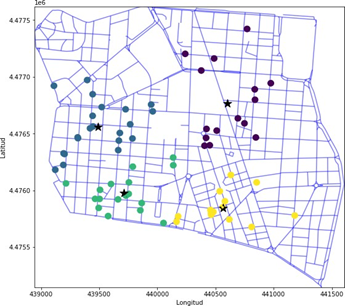
Figura 3. Mapa de FIG 2 con cuatro clústers basado en las coordenadas UTM30 de los bares en Chamberí separados con regiones demarcadas por Voronoi
3.1. Implicación del código e hipótesis iniciales
Con la visualización del código finalmente nos quedan delimitado el distrito de Chamberí en cuatro grupos (clústers) distintos, los cuales llamaremos clúster A (azul), clúster B (morado), clúster C (verde) y clúster D (amarillo). También podemos dividir el distrito en forma de Norte - Sur:
Figura 4. Mapa completo de Chamberí separando los datos en grupos, clúster, delimitación del mapa a modo de Norte-Sur y leyenda completa sobre la gráfica
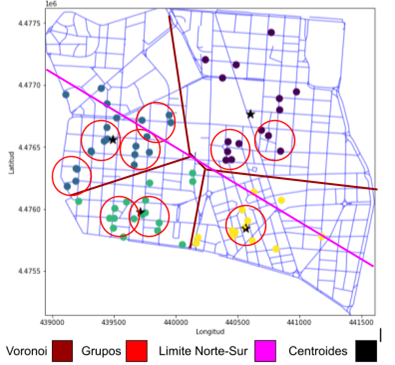
Ahora que hemos identificado los grupos de bares que hay dentro de cada clúster es cuando debemos identificar las preguntas claves que determinarán las posibles ubicaciones idóneas para un nuevo bar dentro del distrito teniendo en cuenta los datos reales disponibles:
- ¿Por qué los clústers de la derecha A y C tienen mayor concentración y grupos de bares que el lado izquierdo del mapa con los clústers B y D?
- ¿Por qué la región Sur de Chamberí tiene una mayor concentración de bares en comparación a la región Norte?
- ¿La densidad de bares implica necesariamente el éxito de la región Sur en contraposición con la región Norte?
- ¿Los grupos de bares en cada clúster indican similitud o indican éxito en venta de ese espacio dentro del cluster? ¿En caso que no sea ninguna de las dos entonces qué implicancia tiene?
- ¿Por qué la mayor parte de los grupos dentro de los clústers tienen como mínimo cuatro bares?
- ¿Por qué hay poca densidad de bares en el norte del clúster A, en el sur del clúster B y en el este del clúster D?
- Teniendo en cuenta toda la información anterior y basándonos en el mapa ¿cuál podría ser la mejor zona para colocar un bar dentro del distrito de Chamberí
3.2. Análisis deductivo sobre la información implícita de los datos
Ahora, buscando responder a cada una de las hipótesis previamente planteadas con la información disponible se tiene lo siguiente:
1. Los clústers A y C tienen mayor densidad de datos en comparación con los clústers B y D debido a que si se revisa el mapa de Chamberí buscando en Google Maps usando las claves “clínicas en Chamberí”, “colegios en Chamberí” y “discotecas en Chamberí” Google Maps nos mostrará los datos geográficos de ese tipo de empresas. Al ser un análisis más deductivo que cuantitativo no necesitamos las coordenadas de cada uno de esos datos, sino más bien delimitamos con una circunferencia tal como se hizo con los grupos dentro de los clústers, así podemos modificar el mapa para agrupar las zonas del distrito de Chamberí que contienen más clínicas y/o hospitales, colegios y discotecas. Esta información se usará para buscar una correlación entre la densidad de bares con sus cercanías.
Figura 5. Discotecas en Chamberí
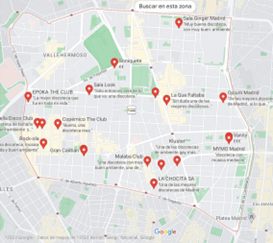
Fuente: Google Maps
Figura 6. Colegios en Chamberí
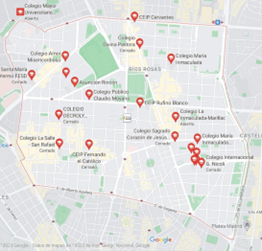
Fuente: Google Maps
Figura 7. Clínicas y hospitales en Chamberí
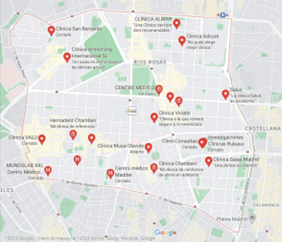
Fuente: Google Maps
Figura 8. Mapa de Chamberí con clústers de los puntos (bares) y circunferencias como zonas de empresas relevantes para el estudio: colegios, hospitales y/o clínicas y discotecas
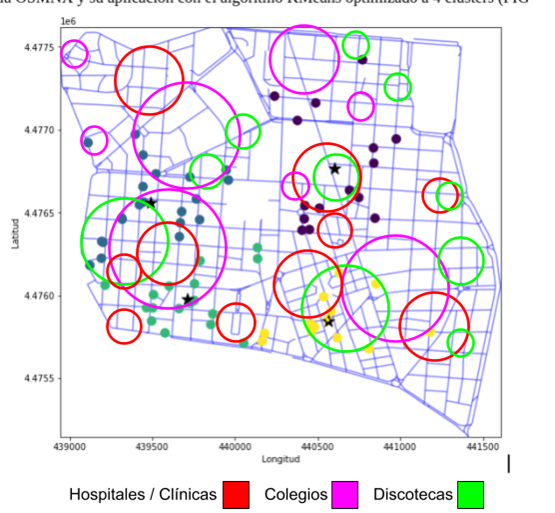
2. Gracias a la información que nos proporciona la respuesta anterior podemos inferir sobre las siguientes respuestas ya que logramos obtener la información implícita relevante:
- Hay más bares en la zona “Sur” de Chamberí respecto a la norte ya que hay mayor concentración de colegios y discotecas.
- Dada la información disponible, la densidad de bares cerca de colegios y discotecas mayormente en los clusters A, C y D implica que estos puedan tener más éxito que los bares del cluster B. Si bien se necesita más información para llegar a dicha conclusión, parece que los clústers A y C tienen una competencia más directa que puede dejar por fuera nuevos bares.
- El mercado en los clústers A y C está saturado por la competencia, debido a su densidad de grupos cercanos de entre 4 a 6 bares, siendo más difícil establecer un bar que pueda ofrecer un servicio diferencial frente a la competencia existente.
3. Sabiendo toda la información disponible con el análisis deductivo implícita dentro del mapa del distrito de Chamberí. ¿Cuáles son las posibles mejores zonas para abrir posibles nuevos bares?
Teniendo en cuenta los datos disponibles podemos concluir que el bar deberá encontrarse en la zona ‘Norte’ para evitar la competencia directa de la zona ‘Sur’, además estar alejado de clínicas y/o hospitales y cercano de alguna discoteca y/o colegios, esto depende de las cercanías. Por ejemplo: Un bar deportivo puede encajar dentro de las cercanías de un colegio.
Figura 9. Mapa de Chamberí con las zonas según relevancia para establecer el nuevo bar
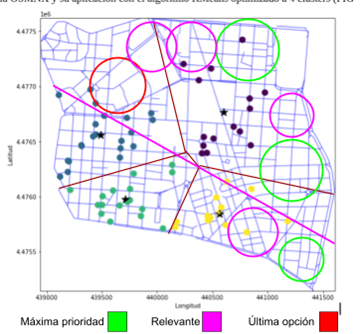
Se han usado estas circunferencias basado a las cercanías para visualizar la relevancia a las zonas cercanas a discotecas, colegios y con menos competencia como zonas de máxima prioridad, las zonas relevantes aquellas con poca cercanía de colegios y discotecas, pero poca competencia con bares cercanos, mientras que las últimas opciones son las zonas con más competencia y/o más cercano de centros médicos como clínicas y hospitales.
Por evitar la competencia directa se descarta por defecto el clúster C y la zona densa del clúster A. El clúster D si cuenta porque cumple con las condiciones para ser una zona de máxima prioridad.
4. Análisis cuantitativo basado en el análisis deductivo de un diagrama Voronoi V(pi) del conjunto de clusters
Una vez obtenido el diagrama de Voronoi con su respectiva aplicación de clústers, división de grupos y deducciones basado en las hipótesis, se debe ahondar con datos sobre las hipotéticas zonas y buscar optimizar dichas zonas bajo un análisis más cuantitativo. Bajo el ejemplo anterior podemos analizar los clusters de forma individual e intentar extraer los datos cuantitativos implícitos en cada uno:
- Los precios que tiene el mercado inmobiliario para la selección del local: permite ver la disponibilidad para la adquisición de una propiedad inmobiliaria y también la relación de oferta demanda comparativamente entre clústers.
- Tener más información sobre el posible poder adquisitivo de la población: con los datos inmobiliarios nos permite hacernos una idea sobre el posible poder adquisitivo de la población, a pesar de que no tengamos esa información de primera mano.
- Reducir la cantidad de potenciales zonas para establecer el nuevo bar: con toda la anterior información obtenida cuantitativamente se puede llegar a una mejor comprensión del contexto, usando Voronoi y la información implícita de los clústers en comparación al uso exclusivo de clusterización sin aplicar Voronoi en unión a los análisis tanto deductivos como cualitativos previos.
En el ejemplo anterior se usó un método deductivo cualitativo para lograr hacer las hipótesis iniciales en base a la información implícita que había disponible para el conjunto de datos del distrito de Chamberí. Para continuar se usará el mismo sistema de Voronoi para ahondar en base a la información implícita de los clústers, sin embargo el enfoque cambiará a un método deductivo cuantitativo con el fin de hacer una mejor estimación y confirmar hipótesis, en este caso se hará uso de los datos de las siguientes tablas, los campos de estas están dividido como TABLA 1 y TABLA 2.
Los datos de la TABLA 1 se han obtenido mediante el trazado de los clústers por filtro de mapa en el portal inmobiliario https://www.idealista.com, mientras que los datos de la TABLA 2 se han obtenido mediante cálculo aritmético explicado posteriormente y el uso de la herramienta web https://www.calcmaps.com/es/map-area/ trazando los clusters para obtener una aproximación de la superficie total de cada clúster:
Tabla 1. Situación inmobiliaria y territorial
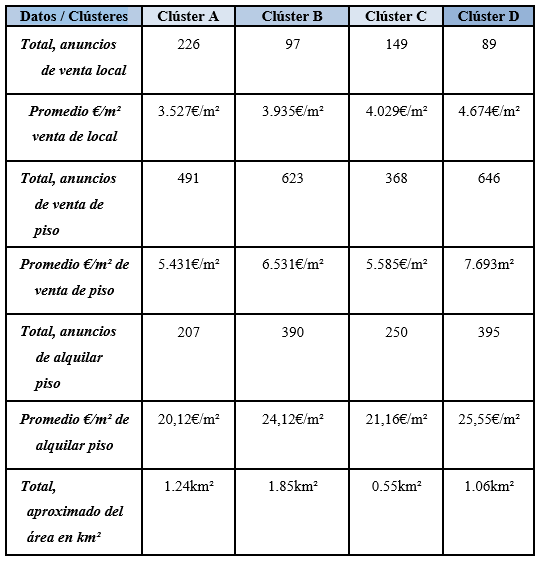
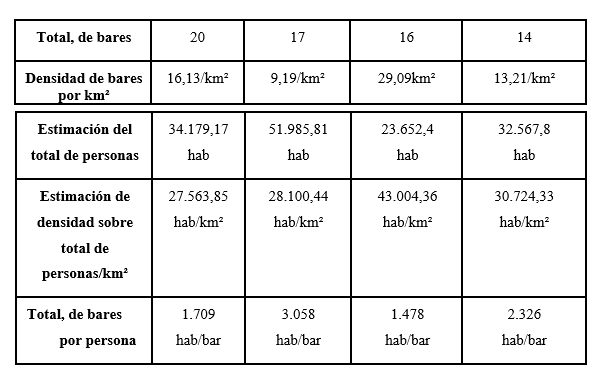
Tabla 2. Situación poblacional y densidad
4.1. Estimación de población:
La población de cada clúster se estima con los datos demográficos ya publicados en el portal estadístico de Madrid, a partir de esto se crea un mapa siguiendo una serie de pasos que se han ido ejecutando hasta ahora:
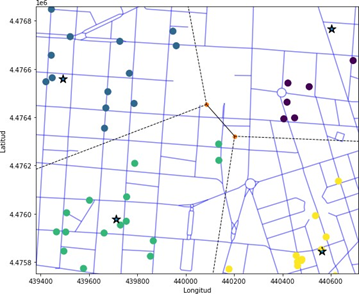
Figura 10. Mapa de Chamberí dividido en: Delimitación político territorial de sus barrios, clusters y subgrupos para dividir la porción del barrio correspondiente a un cluster determinado.
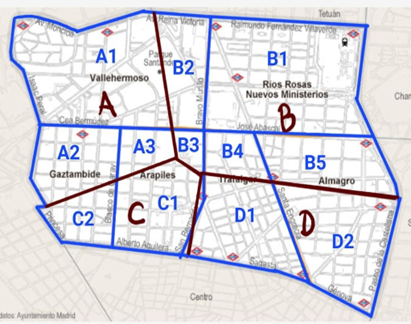
1. Obtener la división político territorial del mapa o en su defecto, la delimitación geoespacial con los datos: Esto para poder transformar dichos datos en un mapa sobre el cual poder trabajar con los datos disponibles. El problema principal de los mapas político territoriales es que su división obedece a una historia o necesidad política, pero no necesariamente sobre la información que pretendemos profundizar.
2. Dividir el mapa como un diagrama de Voronoi y delimitar subgrupos basados en la división político territorial en unión a datos demográficos de dicha división: una vez adquirido el mapa, este se debe marcar un diagrama de Voronoi, en nuestro caso al tratarse del mapa del distrito de Chamberí delimitado por un conjunto de barrios que conforman dicho distrito, entonces se procede a:
- Adquirir la densidad de habitante por km² en los datos demográficos de los barrios que conforman el distrito: consultando los datos demográficos del distrito de Chamberí en unión con los datos geográficos disponibles en el portal estadístico de la comunidad de Madrid https://www.madrid.es/portales/munimadrid/es/Inicio/El-Ayuntamiento/Estadistica/Distritos-en-cifras/Distritos-en-cifras-Informacion-de-Barrios-/?vgnextfmt=detNavegaci on&vgnextoid=0e9bcc2419cdd410VgnVCM2000000c205a0aRCRD&vgnextchannel=27002d05cb71b310VgnVCM1000000b205a0aRCRD se tienen los siguientes datos según el estudio de este mismo portal estadístico a fecha de 2018:
Chamberí = 138.418 hab
Vallehermoso = 18.893,82 hab/km²
Ríos rosas = 27.650,20 hab/km²
Gaztambide = 45.069,44 hab/km²
Arapiles = 42.080,5 hab/km²
Trafalgar = 40.088,24 hab/km²
Almagro = 21.151,50 hab/km²
- Dividir el mapa de los barrios del distrito en subgrupos y que estos formen parte al clúster que le corresponda: esto se logra convirtiendo en subgrupos del clúster las partes de los diferentes barrios que estén dentro del clúster, asignándoles un nombre derivado del propio clúster, cuyo resultado final acabaría siendo similar como la referencia el mapa de la FIG 6, por tanto, la división sería la siguiente:
Vallehermoso:
Forma parte de los clúster A y B, teniendo como subgrupos A1 y B2.
Ríos rosas:
Forma parte del clúster B, teniendo como subgrupo B1.
Gaztambide:
Forma parte de los clúster A y C, teniendo como subgrupos A2 y C2.
Arapiles:
Forma parte de los clúster A, B y C, teniendo como subgrupos A3, B3 y C1.
Trafalgar:
Forma parte de los clúster B y D, teniendo como subgrupos B4 y D1.
Almagro:
Forma parte de los clúster B y D, teniendo como subgrupos B5 y D2.
- Estimar la superficie de los subgrupos de barrios que conforman el distrito:
Para lograrlo se hace uso de la herramienta https://www.calcmaps.com/es/map-area/ con la que podemos estimar la superficie de los subgrupos de clusters basado en los barrios del distrito, con estos datos en conjunto con la densidad de habitantes por barrio de Chamberí son con los cuales se determinará posteriormente la estimación de población por clúster. Sin embargo, al ser una herramienta referencial la precisión que se tenga sobre el trazado en la herramienta tendrá un peso importante sobre el resultado final en la estimación de la población.
A1 = 0,78km², A2 = 0,31km², A3 = 0,13km²
B1 = 1.04km², B2 = 0,32km², B3 = 0,08km², B4 = 0,16km², B5 = 0,35km² C1 = 0,38km² , C2 = 0,17km²
D1 = 0,48km² , D2 = 0,63km²
3. Hacer el cálculo de estimación de población en base al porcentaje que representa los subgrupos de barrios en el clúster y la densidad de población correspondiente:
El cálculo de la estimación de densidad de población se logra haciendo una simple ecuación aritmética en el que se usan los datos disponibles sobre la densidad de habitantes teniendo en cuenta la estimación de superficie de cada subgrupo de clúster basado en los barrios del distrito Chamberí, dando como resultado una estimación más precisa sobre la densidad de habitantes por km² dentro del clúster:
Clúster A = (18.893,82 * 078km²) + (45.069,44 * 0,31km²) + (42.080,5 * 0,13km²) = 34.179,17 hab/km²
Clúster B = (27.650,20 * 1,04km²) + (18.893,82 * 0,32km²) + (42.080,5 * 0,08km²) + (40.088,24 * 0,16km²) + (21.151,50 * 0,35km²) = 51.985,81 hab
Clúster C = (42.080,5 * 0,38km²) + (45.069,44 * 0,17km²) = 23.652,4 hab.
Clúster D = (40.088,24 * 0,48km²) + (21.151,50 * 0,63km²) = 32.567,8 hab.
Este cálculo se usó para obtener los datos disponibles en la TABLA 2 y estos mismos a su vez fueron usados para obtener la estimación del total de personas, la estimación de densidad sobre total de personas/km² y el ratio del total de bares por persona.
Población total clústers = 142.385,18 hab.
Población total Chamberí = 138.418 hab.
4.2. Explicación de los campos y razonamientos
Como se puede observar, ambos resultados son bastante aproximados el resultado a dado una variación Δ = 2,866% lo que significa que este método funciona para estimar adecuadamente la población de un clúster usando solamente los datos implícitos que en este caso de aplicación son los datos demográficos.
Este enfoque es importante ya que en otra clase de ejemplos no se cuenta necesariamente con una delimitación clara con la cual usar de semejante para estudiar el conjunto de datos, en cambio se pueden usar los propios datos en sí junto con Voronoi.
4.3. Reducción de las zonas potenciales
Tras estudiar el ejemplo práctico mediante el análisis cuantitativo se ha podido observar una mejora importante en calidad de la información recabada, siendo un factor determinante el ratio sobre el total de personas por bar (o también densidad personas/bar) en el que a pesar de haber menos oferta disponible de locales a la venta la región del clúster B muestra un mayor potencial de beneficio económico dada la escasa competencia directa y un teórico mayor poder adquisitivo de sus habitantes en una región de Voronoi mayormente de tipo residencial en comparación con los clústers A, C y D debido a los precios de los inmuebles.
Es por ello, por lo que. tomando como referencia el análisis cualitativo anteriormente realizado. podemos optimizar el mapa de zonas relevantes previamente realizado, descartando las zonas señaladas fuera del clúster B.
Figura 11. Mapa de Chamberí con las zonas de relevancia para establecer el nuevo bar, usando de referencia la FIG 9 y los datos del análisis cuantitativo
5. Conclusión
La inclusión de Voronoi en la metodología utilizada para el establecimiento de un nuevo bar en Chamberí ha brindado resultados significativos y reveladores. Al analizar la distribución espacial de los datos y utilizar Voronoi como una herramienta para dividir los clústers en regiones específicas, se logró identificar patrones y correlaciones relevantes.
En particular, se encontró una relación aparente entre la densidad de bares en las proximidades de colegios y discotecas en Chamberí, y su ubicación relativamente alejada de centros médicos. Este hallazgo puede ser de gran utilidad para los tomadores de decisiones y emprendedores interesados en abrir un nuevo bar en esa zona, ya que sugiere una posible oportunidad de mercado al considerar la demanda de locales de entretenimiento nocturno cerca de áreas relevantes
La utilización de Voronoi permitió dividir los datos en regiones claramente delimitadas, lo que facilitó el análisis comparativo y la generación de hipótesis iniciales. Este enfoque deductivo y exploratorio ha demostrado ser eficiente y efectivo para comprender mejor el contexto global de los datos y extraer información valiosa.
Referencias
Computational geometry: An introduction (Franco P. Preparata y Michael Ian Shamos, 1985) Computational Geometry: Algorithms and Applications (en inglés) (tercera edición). Springer-Verlag Berlín Heidelberg. pp. 147-171. ISBN 978-3-540-77973-5.
Inteligencia artificial (IA), Machine Learning (ML) y Deep Learning (DL), manual del alumno 2019. IEDITORIAL código MAN_ED_2393
Referencia de librerías en Python:
OSMnx. (s.f.). OSMnx: Python for street networks. Recuperado el 23 de marzo del 2023, desde https://osmnx.readthedocs.io/en/stable/osmnx.html
Scikit-learn. (s.f.). Clustering. Recuperado el 23 de marzo del 2023, desde https://scikit-learn.org/stable/modules/clustering.html
Scikit-learn. (s.f.). Classes. Recuperado el 23 de marzo del 2023,desde https://scikit-learn.org/stable/modules/classes.html
GeoPandas. (s.f.). GeoPandas: pandas + geometry. Recuperado el 23 de marzo del 2023, desde https://geopandas.org/en/stable/docs.html
Matplotlib. (s.f.). Matplotlib: Visualization with Python. Recuperado el 23 de marzo del 2023, desde https://matplotlib.org/
SciPy. (s.f.). scipy.spatial.Voronoi. Recuperado el 23 de marzo del 2023, desde https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.Voronoi.html
Pyproj. (s.f.). Pyproj. Recuperado el 23 de marzo de 2023, desde https://pyproj4.github.io/pyproj/stable/
Herramientas informáticas usadas como complemento:
Google Colaboratory. (s.f.). Colaboratory. Recuperado el 3 de abril del 2023,desde https://colab.research.google.com/?hl=es
OpenAI. (s.f.). OpenAI Chat. Recuperado el 6 de abril de 2023, desde https://chat.openai.com/
Conversor de coordenadas geográficas UTM. (s.f.). Conversor desde coordenadas decimales a coordenadas geográficas UTM. Recuperado el 23 de marzo del 2023, desde https://franzpc.com/apps/conversor-coordenadas-geograficas-utm.html
Google Maps. (s.f.). Google Maps. Recuperado el 10 de abril del 2023, desde https://www.google.es/maps/?hl=es
Códigos usados de ejemplo en el trabajo
Diego Fonseca (2022). Mall customers clustering - Kmeans and Voronoi. Recuperado el 23 de marzo del 2023, de https://www.kaggle.com/code/zaldiego/mall-customers-clustering-kmeans-and-voronoi
Diego Fonseca. (2023). Geospatial Madrid and Voronoi. Recuperado el 10 de abril del 2023, desde https://www.kaggle.com/code/zaldiego/geospatial-madrid-and-voroni
Referencia en descripción formal de algoritmos
Wikipedia. (s.f.). OPTICS algorithm. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://en.wikipedia.org/wiki/OPTICS_algorithm
Wikipedia. (s.f.). DBSCAN. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://en.wikipedia.org/wiki/DBSCAN
Wikipedia. (s.f.). K-means clustering. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://en.wikipedia.org/wiki/K-means_clustering
Wikipedia. (s.f.). Algoritmo Mean-Shift. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://en.m.wikipedia.org/wiki/Mean_shift
Wikipedia. (s.f.). KNN vecinos cercanos. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://es.wikipedia.org/wiki/K_vecinos_m%C3%A1s_pr%C3%B3ximos
Wikipedia. (s.f.). Voronoi diagram. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://en.m.wikipedia.org/wiki/Voronoi_diagram
Wikipedia. (s.f.). Análisis de grupos. En Wikipedia. Recuperado el 3 de abril del 2023, desde https://es.wikipedia.org/wiki/An%C3%A1lisis_de_grupos
Herramientas usadas en el análisis cuantitativo:
Idealista. (s.f). Portal inmobiliario con filtro de propiedades por mapa. En idealista. Recuperado el 10 de abril del 2023 desde https://www.idealista.com
Calcmaps. (s.f). Portal web de medición de área y superficie de zonas geográficas. En calcmaps. Recuperado el 10 de abril del 2023, desde https://www.calcmaps.com/es/map-area/
Comunidad de Madrid. (s.f). Portal web de Madrid. Recuperado el 10 de abril del 2023, desde https://www.madrid.es/portales/munimadrid/es/Inicio/El-Ayuntamiento/Estadistica/Distritos-en-cifras/ Distritos-en-cifras-Informacion-de-Barrios-/?vgnextfmt=detNavegacion&vgnextoid=0e9bcc2419cdd4 10VgnVCM2000000c205a0aRCRD&vgnextchannel=27002d05cb71b310VgnVCM1000000b205a0a RCRD
Listado de versiones usadas en los códigos:
Python == 3.9.12 Scikit learn == 1.2.2 Pandas == 1.5.3
Matplotlib == 3.5.1
OSMNX == 1.3.0
Numpy == 1.23.5
Scipy == 1.10.1
Geopandas == 0.12.2
Pyproj4 == 3.4.1
Spyder == 5.1.5
Los más leídos
ADRIÀ NOLLA DEL VALLE, (2023)
La Cartera Adaptada: adaptando la cartera permanente a los ciclos económicos Leer InvestigaciónAlberto Conchillo Guantes, (2023)
Impacto del impuesto de sociedades en el comportamiento de las empresas Leer InvestigaciónFrancisco Javier Roldán de la Rosa, (2023)
Historia y evolución de la Farmacovigilancia Leer InvestigaciónRelacionados Informática y TICS
- Data Science y Recursos Humanos: implementando el HR Analytics
- Competitividad & Desarrollo (Perspectiva Descriptiva & De Correlación)
- Tecnología y sus efectos en nosotros
- Análisis del impacto del subsector de la restauración en la contratación del sector turístico en Andalucía. Un estudio por provincias y municipios de la Comunidad Autónoma Andaluza
- Desarrollo e implantación de sistema de soporte de decisión en líneas de producción de PACKSNAK, S.L.
- Diseño e implementación de un Datawarehouse en una cadena de tintorerías y lavanderías
- Analizando la cadena de bloques en materia de ciberseguridad con diseño de un “smart contract” para el despliegue de token criptográfico y su uso con transacciones sobre “Wallets” para el conjunto de empleados de una organización sobre Blockchain Pública
- Estudio, análisis y desarrollo de herramientas de las distintas fases del hacking ético
- Hacking Ético en Redes Wifi
- Yaaseen Oman: desarrollo y puesta en producción de una aplicación web